Ces surfaces sont, comme leur nom l'indique, les surfaces dont les lignes de courbures sont planes.
 

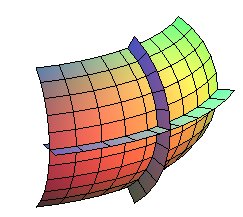
D'après un théorème de Joachimstahl, la courbe d'intersection d'une surface avec un plan est une ligne de courbure si et seulement si le plan fait un angle constant avec la surface le long de cette courbe (voir la page sur les lignes de courbure). Ci-contre, exemple d'une surface de révolution où les plans des parallèles et des méridiennes coupent la surface à angle droit.

 
 

Equation aux dérivées partielles (notation de Monge) :

Exemples :
   - les cylindres où les lignes de courbure sont les génératrices et leurs trajectoires orthogonales
   - les surfaces de révolution où les lignes de courbure sont les parallèles et les méridiennes
   - les surfaces moulures, qui contiennent les précédentes ; ce sont les surfaces à lignes de courbure planes dont l'une des familles est formée de courbes parallèles
   - les cyclides de Dupin, qui sont les surfaces dont les lignes de courbures sont circulaires ou rectilignes.
 

surface suivante

surface précédente

courbes 2D

courbes 3D

surfaces

fractals

polyèdres

© Robert FERRÉOL  2020